Hình chiếu là gì? Nghe có vẻ rất đơn giản vì đây là kiến thức của Toán Học lớp 7. Nhưng không phải ai cũng có thể hiểu về khái niệm này một cách chính xác.
Hãy cùng tham khảo bài viết dưới đây của Hytcc.org.vn sẽ giải đáp cho bạn một cách chi tiết về hình chiếu.
Hình chiếu là gì?
Hình chiếu là hình biểu diễn ba chiều của vật lên mặt phẳng hai chiều. Yếu tố cơ bản giúp tạo nên hình chiếu chính là vật cần chiếu, phép và mặt phẳng chiếu.
Hình chiếu của một đoạn thẳng nằm trên đường thẳng chính là khoảng cách giữa hai đoạn thẳng vuông góc với đường thẳng đã cho trước. Hình chiếu của một điểm tức là giao điểm của đường thẳng đã cho trước, và đường thẳng kẻ từ điểm vuông góc.
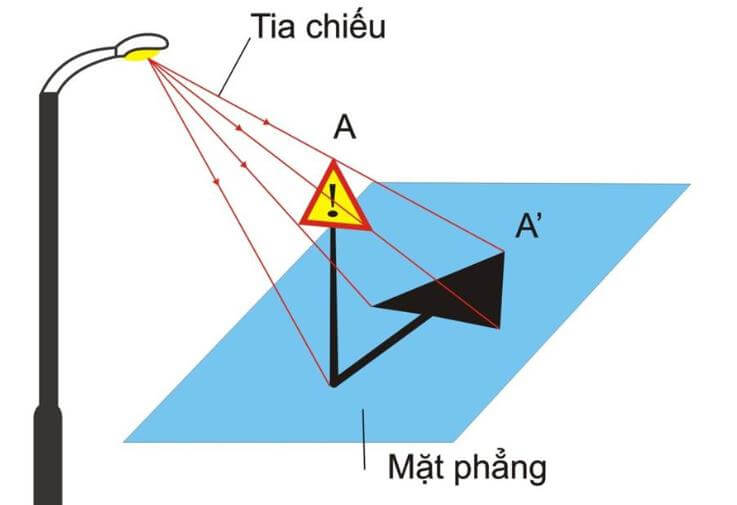
Phân loại hình chiếu
Hiện nay chúng ta có tổng gồm 2 loại hình chiếu đó là hình chiếu thẳng góc và hình chiếu trục đo. Dưới đây là kiến thức chi tiết về 2 loại hình chiếu này:
1. Hình chiếu thẳng góc
Đây là loại hình biểu diễn theo cách đơn giản, hình dạng, kích thước của vật thể đã được bảo toàn và cho phép thể hiện hình dạng, kích thước vật thể một cách chính xác.
Với mỗi hình chiếu thẳng góc sẽ chỉ thể hiện được hai chiều. Nên chúng ta cần phải dùng đến nhiều hình chiếu để biểu diễn nhất là đối với những vật thể phức tạp. Có ba hình chiếu phổ biến đó là: Hình chiếu đứng, hình chiếu cạnh và hình chiếu bằng.
2. Hình chiếu trục đo
Hình chiếu này có thể biểu diễn được hết ba chiều của vật thể lên trên mặt phẳng chiếu. Và các tia chiếu song song với nhau. Sẽ tùy vào phương chiếu là vuông góc hay xiên góc. Theo sự tương quan của ba chiều, sẽ được phân ra các loại hình chiếu như sau:
a. Hình chiếu trục đo vuông góc
- Hình chiếu trục đo vuông góc, có đều ba hệ số biến dạng với ba trục bằng nhau
- Hình chiếu trục đo vuông góc sẽ cân hai trong ba hệ số biến dạng, có từng đôi một bằng nhau
- Hình chiếu trục đo vuông góc sẽ lệch ba hệ số biến dạng, với ba chục không bằng nhau
b. Hình chiếu trục đo xiên góc
- Hình chiếu trục đo xiên góc đều
- Hình chiếu trục đo xiên góc cân
- Hình chiếu trục đo xiên góc lệch
Tam giác hình chiếu là gì?
Tam giác hình chiếu hay còn được gọi là tam giác bàn đạp tại điểm P với tam giác đã cho trước và có ba đỉnh là hình chiếu của điểm P lên ba cạnh của tam giác.
Với mỗi điểm P sẽ có một tam giác bàn đạp khác nhau, ví dụ:
- Nếu P = trực tâm, thì LMN = tam giác orthic
- Nếu P = tâm nội tiếp, thì LMN = tam giác tiếp xúc trong
- Nếu P = tâm ngoại tiếp, thì LMN = tam giác trung bình
Khi P nằm trên đường tròn ngoại tiếp, lúc này tam giác bàn đạp sẽ trở thành một đường thẳng.
Quan hệ giữa đường vuông góc với đường xiên, và đường xiên với hình chiếu
Cho một điểm A nằm bên ngoài đường thẳng d, sau đó kẻ một đường thẳng vuông góc tại điểm H và trên d lấy điểm B không trùng với điểm H. Ta có:
- Đoạn thẳng AH: Được gọi là đoạn vuông góc hay còn là đường vuông góc bắt đầu kẻ từ A đến đường thẳng d
- Điểm H: Là đường xiên góc bắt đầu kẻ từ A đến đường thẳng d
- Đoạn thẳng AB: Là đường xiên góc bắt đầu kẻ từ điểm A đến đường thẳng d
- Đoạn thẳng HB: Là hình chiếu của đường xiên góc AB ở trên đường thẳng d
Định lý 1: Trong các đường xiên góc và trong đường vuông góc kể từ điểm nằm ngoài đường thẳng, cho đến đường thẳng đó, đường vuông góc sẽ là đường ngắn nhất.
Định lý 2: Trong hai đường xiên góc kể từ điểm nằm ngoài đường thẳng cho đến đường thẳng đó:
- Đường xiên góc có hình chiều lớn hơn, tương đương sẽ lớn hơn.
- Đường xiên góc lớn hơn, sẽ có hình chiếu lớn hơn.
- Hai đường xiên góc bằng nhau, hai hình chiếu sẽ bằng nhau. Hai hình chiếu bằng nhau thì hai đường xiên góc bằng nhau.
Đây đều là những kiến thức vô cùng cần thiết và quan trọng cho các bạn học sinh để áp dụng vào các bài toán trong chương trình học của mình. Hãy thường xuyên luyện tập các kỹ năng thực hành giải toán chắc chắn bạn sẽ trở thành một học sinh ưu tú.
Hy vọng bài viết trên của Hytcc.org.vn đã giúp mọi người có thể hiểu rõ hơn về hình chiếu là gì? Cách phân loại hình chiếu. Để tìm kiếm thêm các thông tin liên quan, cũng như trau dồi thêm một số kiến thức trong các lĩnh vực khác nhau. Hãy thường xuyên ghé thăm website của chúng tôi để cập nhật những thông tin vô cùng bổ ích. Chúc các bạn thành công!



