Xin chào các bạn! Tiếp tục với chuyên mục chia sẻ lý thuyết Toán học thì trong bài viết ngày hôm nay. Hytcc.org.vn sẽ chia sẻ với các bạn về một định lý về tỷ lệ, đó chính là định lý Talet.
Đây là một định lý rất quan trọng trong hình học về tỷ lệ giữa các đoạn thẳng trên hai cạnh của một tam giác bị chắn bởi một đường thẳng song song với cạnh thứ 3. Và để tìm hiểu rõ hơn về nội dung của định lý Talet. Mời các bạn cùng theo dõi bài viết dưới đây nhé.
Tỉ số của hai đoạn thẳng là gì?
Trước khi bắt đầu tìm hiểu về định lý Talet, chúng ta sẽ cùng nhắc qua về tỉ số của hai đoạn thẳng đã các bạn nhé.
- Tỉ số của 2 đoạn thẳng là tỉ số độ dài của chúng theo cùng một đơn vị đo. Và tỉ số của 2 đoạn thẳng sẽ không phụ thuộc vào cách chọn đơn vị đo.
- Tỉ số của 2 đoạn thẳng AH và BE sẽ được kí hiệu là AH/BE.
Ví dụ: Cho đoạn thẳng AB và một tỉ số m/n > 0. Điểm C thuộc AB biết CA/CB = m/n. Khi đó, ta gọi điểm C là điểm chia đoạn thẳng AB theo tỉ số m/n.
Đoạn thẳng tỉ lệ
Giả sử chúng ta có 2 đoạn thẳng AB và CD. Hai đoạn thẳng này được gọi là tỉ lệ với 2 đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức: AB/CD = A’B’/C’D’ hay AB/A’B’ = CD/C’D’.
Định lý Talet trong tam giác
1. Định lý Talet thuận
Định lý Talet thuận sẽ được phát biểu như sau:
Nếu có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
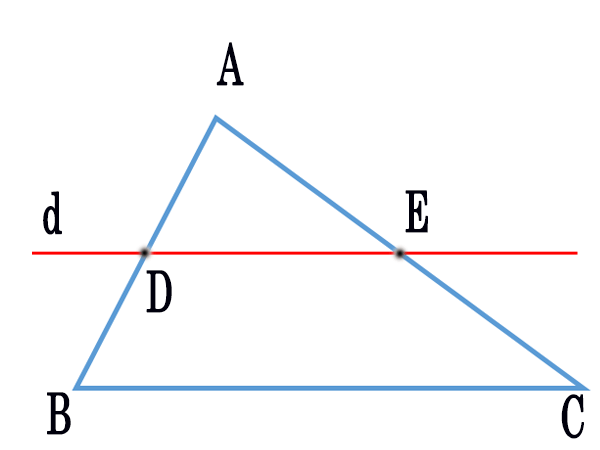
Ví dụ: Cho tam giác ABC, đường thẳng d cắt AB tại D, cắt AC tại E và song song với BC.
Theo định lý Talet, ta có:
2. Định lý Talet đảo
Định lý Talet đảo sẽ được phát biểu như sau:
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác.
Ví dụ: Với hình minh họa như trên, nếu trong tam giác ABC ta chứng minh được các cạnh có tỉ lệ giống như 1 trong 3 tỉ lệ trên thì theo định lý Talet đảo sẽ suy ra: DE // BC.
Hệ quả của định lý Talet
Được phát biểu như sau:
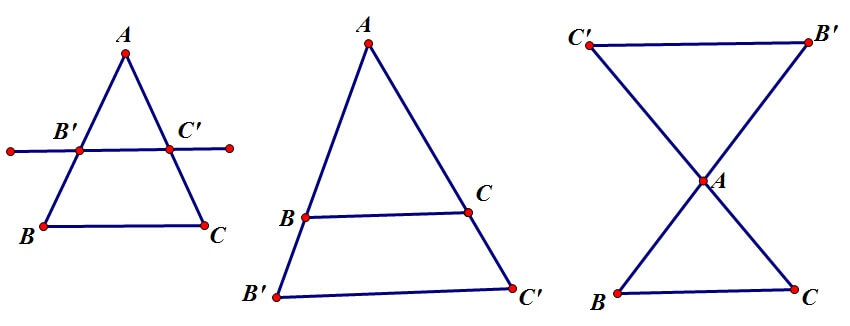
- Hệ quả 1: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 cạnh tam giác đã cho
- Hệ quả 2: Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu
- Hệ quả 3 – Talet mở rộng: Nếu 3 đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tương ứng tỉ lệ
Định lý Talet trong hình thang
Được phát biểu như sau:
Nếu có một đường thẳng song song với 2 cạnh đáy của hình thang và cắt 2 cạnh bên của hình thang thì nó sẽ định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
Ví dụ: Cho hình thang ABCD như hình dưới:
Trong hình thang ABCD, E thuộc AD, F thuộc BC.
Nếu EF // AB // CD thì ta có: AE/DE = BF/CF.
Ngược lại, nếu: AE/DE = BF/CF thì ta có thể suy ra: EF // AB // CD.
Định lý Talet trong không gian
Ba mặt phẳng song song chắn trên hai đường thẳng d1, d2 những đoạn thẳng tỉ lệ:
Định lý đảo của định lý Talet trong không gian:
Các dạng toán thường gặp
Dạng 1: Tính độ dài của đoạn thẳng, chu vi, diện tích và các tỉ số
Phương pháp:
Để giải các bài toán dạng này, ta sử dụng định lý Talet, hệ quả của định lý Talet và tỉ số đoạn thẳng để tính toán nhé.
- Định lý: nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ
- Hệ quả: nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 cạnh tam giác đã cho
Ngoài ra, chúng ta còn có thể sử dụng đến tính chất của tỉ lệ thức:
Dạng 2: Chứng minh hai đường thẳng song song, chứng minh các đẳng thức hình học.
Để giải các bài toán thuộc dạng này, chúng ta sẽ sử dụng định lý Telet, định lý Talet đảo và hệ quả của định lý Talet để chứng minh nhé.
Như vậy, trên đây là những kiến thức có liên quan đến định lý Talet cực kỳ chi tiết mà mình đã chia sẻ với các bạn. Hy vọng rằng những kiến thức này sẽ giúp bạn hiểu rõ hơn về định lý Talet cũng như có thể sử dụng định lý Talet thành thạo để giải các bài toán liên quan nhé. Cảm ơn các bạn đã dành thời gian theo dõi bài viết. Chúc các bạn học tập thật tốt!